Fall Challenge 2020

Fall Challange 2020 est un challenge proposé par CodingGame. Un moyen ludique et gratifiant pour apprendre à utiliser certains principes essentiel en programmation. Ici, voici une petite explication sur tout ce qui m'a permis d'atteindre le rang 20~
@Noé Toniolo
Dernière modification : 03 March 2023 a year ago

Lien du challenge

Voici une petite explication de mon code qui m'a permis d'atteindre le rang ~30.

C'est un guide qui explique seulement les principes intéressants utilisés durant ce challenge :

  • la création optimisée d'un graphe
  • Beam Search
  • Utilisation du binaire pour définir et gérer un état
  • la pratique TDD

Si vous suivez bien le guide, et que vous avec un environnement de développement solide (TDD), vous devriez aisément atteindre un rang ~50, et même, plutôt rapidement

Si vous poussez un peu plus loins, que cela soit

  • Améliorer l'algo
  • Simuler les tours suivant de votre adversaire
  • l'utilisation de cg-brutaltester pour affiner sa fonction d'évaluation
  • L'exploration des referees

Vous pourrez sans aucun doute monter bien plus haut !

Notes importantes

Compétences requises

  • Il est impératif de bien comprendre les règles du jeu.
    • Codez votre propre dummy bot afin d'accéder â la ligue bronze
  • Il est important d'être familier avec les opérations binaires

Autres

  • Vous pouvez indiquer au compilateur d'activer ses flags d'optimisation en ajouter cette petite ligne

    #pragma GCC optimize("O3", "unroll-loops", "omit-frame-pointer", "inline")

  • Vous pouvez utiliser mon template de projets CG gc_cpp_template
    • Lisez bien le README afin d'utiliser codingame-sync avec cpp-merge

Comment éviter les états dupliqués

On entre directement dans le vif du sujet

L'intérêt

Un état de jeu peu être traduit sous forme d'un entier avec 64 bits, et c'est idéal afin de pouvoir stocker l'état dans un hash set. L'intérêt va être d'éviter les "collisions".

Par exemple depuis un état X, je peux faire

  • X1 -> REST + LEARN 12.
  • X2 -> LEARN 12 + REST

Ces deux sous enfants d'un même état seront alors similaires.

Grâce à notre CompactState, on va pouvoir vérifier dans le HashSet si cet état existe déjà, et si c'est le cas, pas besoin d'ajouter cet état dans notre graphe !

De ce fait, en évitant d'inclure bon nombre d'états similaires, nous allons pouvoir explorer bien plus profondément.

Pour information, je regarde un tour au hasard d'une de mes parties, et sur 30000 états éludés jusqu'à une profondeur de 26 tours, j'ai pu éviter 88000 états dupliqués (ce qui représente enfaite bien plus d'esquive, car chacun de ces états aurait donc généré ses propres enfants doublement dupliqués ect !)

CompactState

Les possibilités que m'offre les règles du jeu, un état, peuvent être stocké sous forme de bits.

On prendra en compte uniquement notre situation (nous nous trouvons à gauche), et nullement celui de l'adversaire.

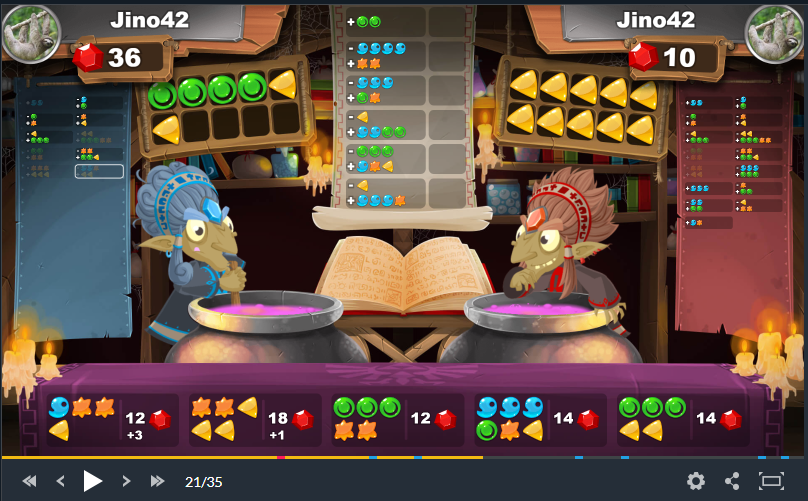
Voici l'état de référence pour tous nos exemples :

Référence

Spells

Dans cet exemple, je peux caster avec :

  • Le spell 1 ?
  • Le spell 2 ?
  • Le spell 3 ?
  • Le spell 4 ?
  • ...

Nostale emoji Attention, je parle ici bien du fait si le spell est oui ou non castable et non pas si j'ai les ingrédients ou la place nécessaire pour caster le spell. Nostale emoji

Le jeu peu nous offrir jusqu'à 42 spells supplémentaires, avec les 4 premiers spells de base, cela nous fait potentiellement 46 spells que l'ont peu disposé dans notre sac !

Néanmoins, un tel scénario n'a sans aucun doute quasi aucune chance d'y arriver.

Pour des contraintes que je développerais en dessous, je pars du principe que nous pouvons avoir dans notre sac jusqu'à 31 spells.

Dans notre entier 64 bits, je réserve 31 bits pour mes spells.

En se référant a notre exemple, cela donnerait :

000 0000  0000 0000  0000 0001  0011 1100

Brews

De même, est-ce je peux brew :

  • La recette 1 ?
  • La recette 2 ?
  • ...

Alors, à première vue, on peut se dire que la réponse sera toujours fausse.

Ce qui est vrai pour l'état initial du jeu. Mais lorsque nous allons exécuter de multiples actions et descendre en profondeur dans notre graphe, les états enfants pourront avoir des brews déjà utilisés.

Comme nous ne pouvons savoir quel sera le prochain brew, ou le prochain spell dans le grimoire, nous partons du principe qu'ils ne seront pas remplacés !

Je réserve 5 bits pour les brews :

0 0000

Learns

De meme, est-ce que le spell a déjà été learn :

  • Le spell 1 ?
  • La spell 2 ? ...

Je réserve 6 bits pour les learns

00 0000

Learned

Et oui ! Les spells learned dans un état parent peuvent être utilisé dans un état enfant.

Imaginons que nous apprenons le spell 2 dans le grimoire :

Nos Learn bits vaudront : 00 0010

Nos Learned bits vaudront : 00 0010

Le comportement des Learned bits est similaire aux Spells bits !

Inventaire

L'inventaire est limité à 10 ingrédients. Il existe 4 types d'ingrédients.

Il nous faut minimum 4 bits pour pouvoir stocker le nombre d'ingrédients existant dans l'inventaire. Et nous avons 4 ingrédients

Je réserve donc 16 bits

t4=2 t3=0 t1=4 t1=0
0010 0000 0100 0000

Assembler chaque élément

Légende

b -> brew
l -> learn
a -> clast learned
s -> spells castable
i -> inventaire

Vous pouvez gérer vos data de deux manières :

  • Avoir une variable pour chaque élément (cf Data désunifié)
  • Avoir une seule variable pour tous les éléments (cf Data unifié)

Data désunifié

b :                                 0 0000
l :                                00 0000
a :                                00 0000
s : 000 0000 0000 0000 0000 0000 1001 1110
i :                    0010 0000 0100 0000 
                       t4=2 t3=0 t2=4 t1=0

Data unifié

0010 0000  0100 0000  0000 0000  0000 0000  0000 0001  0011 1100  0000 0000  0000 0000
iiii iiii  iiii iiii  ssss ssss  ssss ssss  ssss ssss  ssss sssa  aaaa alll  lllb bbbb
t4=2 t3=0  t2=4 t1=0

Les deux approches sont tout à fait viable pour la gestion des états (Lorsque vous allez effectuer vos actions brews/learn/cast/...), a vous de voir votre préférence. Vous allez avoir besoin de la Data unifié, qui sera votre Key dans la HashMap. Il suffira juste de recomposer celle-ci. (cf Bitwise opérations)

Dans mon cas, j'utilise les deux approches en même temps.

Soit, s-a-l-b unifié et mon inventaire désunifié

Quelques exemples d'états :

Depuis notre état de référence ;

Si on exécute l'action brew sur la troisième recette, alors l'état de l'enfant ressemblera à ceci :

0010 0001  0011 0000  0000 0000  0000 0000  0000 0001  0011 1100  0000 0000  0000 0100
iiii iiii  iiii iiii  ssss ssss  ssss ssss  ssss ssss  ssss sssa  aaaa alll  lllb bbbb
t4=2 t3=1  t2=3 t1=0

Puis si on learn le spell numéro 1 et qu'on le cast juste après, l'enfant n+3 ressemblera à ceci :

0001 0010  0011 0011  0000 0000  0000 0000  0000 0001  0011 1100  0000 1000  0010 0100
iiii iiii  iiii iiii  ssss ssss  ssss ssss  ssss ssss  ssss sssa  aaaa alll  lllb bbbb
t4=1 t3=2  t2=3 t1=3

Wikipedia

En informatique, la recherche en faisceau est un algorithme de recherche heuristique qui explore un graphe en ne considérant qu'un ensemble limité de fils de chaque nœud. La recherche en faisceau est une optimisation de l'algorithme de parcours en largeur, en réduisant la mémoire nécessaire à son exécution. Contrairement à l'algorithme best-first où l'on explore tous les états candidats à la solution recherchée en

Afin de rendre une solution à chaque tour, nous allons éluder et évaluer chaque action possible.

Pour gagner en performances, nous allons créer conteneur avec déjà toute la mémoire mappée que nous souhaitons.

Dans mon cas, j'ai voulu être large, j'ai un conteneur d'une taille de 100 000 nodes.

Chacun de ces nodes est défini ainsi :

class Node {    Node *parent;    CompactState state;    Action action;    uint depth;    int evaluationScore;    uint spellLearned;};

Pour chaque état, nous allons essayer de créer tous ses enfants possibles via toutes les actions possibles

Nostale emoji Je vous conseille d'appréhender le code en commençant par la fonction doBeamSearch Nostale emoji

    class Resolver {        GameState &game; // L'objet qui détient toutes les données de notre jeu. C'est-à-dire nos joueurs, leurs spells, brews et learns avec toutes les données utiles                vector<Node> candidateNodesOfCurrentDepth; // Une fois tous les nodes d'une profondeur éludée, on les évalue et on ne garde que les meilleurs qui seront placés dans notre conteneur nodes           // Ici seront stockés les nodes éludé et évalué qui pourront constituer un résultat        // On ajoute des nodes a notre container seulement dans la fonction init() qui va ajouter notre état de départ        // Puis dans la fonction increaseDepth(), où on va ajouter les meilleurs nodes de la current depth        vector<Node> nodes;                HashSet<uint64_t> hashSet;        int totalResolvedNodes;        int currentResolvedNodesToTreat;        int currentDepth;                        // Constructeur        Resolver() {            // Afin d'optimiser, on alloue directement la masse de mémoire !            candidateNodesOfCurrentDepth.reserve(X);            nodes.reserve(Y);        }           void init() {            totalResolvedNodes = 0;            currentResolvedNodesToTreat = 0;            currentDepth = 0;            maxScore = 0;            Node &initialNode = nodes[totalResolvedNodes++];            CompactState initialCompactState = game.toCompactState(); // CompactState toujours relatif a mon joueur            initialNode = Node(initialCompactState, nullptr, Action(Action::None));            hashset.add(initialNode.state.getHash());        }        void generateNewChildFromAction(currentNode, action) {            childState = currentNode.state.generateCompactStateOnDoAction(game, action);            if (!hashSet.exist(childState.getHash())) {                Node childNode = Node(childState, &currentNode, action); // Node(CompactState childCompactState, Node *parentNode, Action action);                candidateNodesOfCurrentDepth.push_back(childNode); // N'hésitez pas a utiliser emplace_back                hashSet.add(childNode.state.getHash());            }            // Sinon, le state existe déjà dans l'hashSet. On ne fait rien pour éviter les duplicas et on passe à la suite !        }        void generateAllChildStates(Node const &currentNode) {            // BREW            for (int i = 0; i < MAX_BREW_SIZE; i++) { // MAX_BREW_SIZE == 5                if (currentNode.state.canBrew(game, i)) {                    generateNewChildFromAction(currentNode, Action(Action::BREW, i));                }            }            // CAST            for (int i = 0; i < game.me.spells; i++) { // Pour chaque spell que je détiens                int repetable = 0;                // canCast prends la référence de repetable.                // Dans mon implémentation, j'ai choisi de prendre en compte seulement la possibilité ou je cast le plus.                // Mais il est tout à faire possible de générer plusieurs solutions pour [1, repetable]                if (currentNode.state.canCast(game, i, repetable)) {                      generateNewChildFromAction(currentNode, Action(Action::CAST, i, repetable));                }            }            // LEARN            for (int i = 0; i < MAX_LEARN_SIZE; i++) { // MAX_LEARN_SIZE == 6                if (currentNode.state.canLearn(game, i)) {                      generateNewChildFromAction(currentNode, Action(Action::LEARN, i));                }            }            // CAST un spell déjà LEARN            for (int i = 0; i < MAX_LEARN_SIZE; i++) { // MAX_LEARN_SIZE == 6                if (currentNode.state.canCastLearned(game, i)) {                      generateNewChildFromAction(currentNode, Action(Action::CAST_LEARNED, i));                }            }            // REST            if (currentNode.state.canRest()) {                  generateNewChildFromAction(currentNode, Action(Action::REST));            }        }        // Évalue tous les candidats        // Garde les nodes avec les meilleurs evaluationScore        // augmente la profondeur        void increaseDepth() {            // On évalue le score pour chaque enfant généré pour la profondeur actuelle, et on garde le meilleur Node au passage            for (int i = 0; i < candidateNodesOfCurrentDepth.size(); i++) {                Node &candidateNode = candidateNodesOfCurrentDepth[i];                candidateNode.state.evaluate(game, candidateNode);                candidateNode.evaluationScore = (candidateNode.parent ? candidateNode.parent->evaluationScore : 0.0f)                                                 + (candidataNode.evaluationScore * pows[candidateNode.depth]);               if (candidateNode.evaluationScore > maxScore) {                   maxScore = candidateNode.evaluationScore;                   best = candidateNode;               }            }           sort(candidateNodesOfCurrentDepth.begin(), candidateNodesOfCurrentDepth.end(), [](Node const &a, Node const &b) -> bool {               return a.evaluationScore > b.evaluationScore;           });           // On ne garde que les 1700 meilleurs résultats dans mon cas           for (int i = 0; i < MAX_KEEP_PER_DEPTH && i < candidateNodesOfCurrentDepth.size(); i++) {               nodes[totalResolvedNodes++] = candidateNodesOfCurrentDepth[i];           }           // On augmente alors le niveau de profondeur pour passer au tour suivant !           candidateNodesOfCurrentDepth.clear();           currentDepth++;        }        void doBeamSearch() {            Stopwatch watch;            init();            // Parcours chaque element éludé et évalué de notre container nodes            while (watch.msTime() < MAX_MS                   && (queueCount > queueIndex || candidateNodesOfCurrentDepth.size())) {                                 // Si nous n'avons plus de Node a explorer                if (totalResolvedNodes == currentResolvedNodesToTreat) {                    increaseDepth();                }                                // On prends le prochain node dans la queue, et on élude tous ses enfants qui deviendrons des candidats potentiel                Node *currentNode = &nodes[queueIndex++];                generateAllChildStates(currentNode);           }       }   }

Fonction d'évaluation

Ma fonction d'évaluation est classique

  • 1.2 points pour chaque point de score (les rubys que m'apportent les brews, et le score qu'apporte l'inventaire)
  • 2 points pour chaque ingrédient vert dans mon inventaire
  • 3 points pour chaque ingrédient orange dans mon inventaire
  • 3.5 points pour chaque ingrédient jaune dans mon inventaire
  • 1 point pour chaque LEARN

Il peut être intéressant de faire en sorte que plus on plonge en profondeur, plus le score de l'évaluation soit amoindri Cela donne plus d'importance aux opérations qui cherchent des points un peu plus rapidement

parent->evaluationScore + evaluationScore * 0.97 ^ depth;

Selon la performance de votre algo, vous pouvez modifier la largeur de votre Beam Search. Plus il est grand, plus on garde une grande quantité de candidats, moins il va loin.

À une largeur de 1000, mon algo va parfois jusqu'à une profondeur de 45 ! (Ce qui est bien trop profond évidemment !)

À vous de trouver largeur qui vous convient :)

TDD

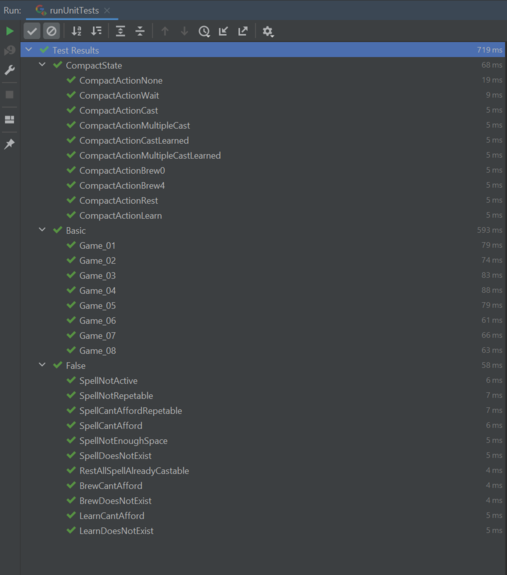
TDD

Dans notre cas, nous souhaitons tester toutes nos actions possibles.

Pour construire nos tests, nous allons devoir récupérer les inputs envoyés à notre bot afin de le stocker dans un fichier test.

C'est une étape absolument INDISPENSABLE, de quoi gagner du temps et de la confiance !

Cela va nous permettre aussi de réfactorer ou optimiser notre code

J'ai utilisé la librairie googletest pour mar part.

Par exemple :

28
51 BREW -2 0 -3 0 14 3 3 0 0
62 BREW 0 -2 0 -3 17 1 4 0 0
64 BREW 0 0 -2 -3 18 0 0 0 0
52 BREW -3 0 0 -2 11 0 0 0 0
49 BREW 0 -5 0 0 10 0 0 0 0
0 LEARN -3 0 0 1 0 0 1 0 1
1 LEARN 3 -1 0 0 0 1 1 0 1
40 LEARN 0 -2 2 0 0 2 0 0 1
34 LEARN -2 0 -1 2 0 3 0 0 1
38 LEARN -2 2 0 0 0 4 0 0 1
18 LEARN -1 -1 0 1 0 5 0 0 1
78 CAST 2 0 0 0 0 -1 -1 0 0
79 CAST -1 1 0 0 0 -1 -1 1 0
80 CAST 0 -1 1 0 0 -1 -1 1 0
81 CAST 0 0 -1 1 0 -1 -1 0 0
86 CAST 0 3 2 -2 0 -1 -1 1 1
88 CAST 0 0 -3 3 0 -1 -1 1 1
90 CAST -2 0 1 0 0 -1 -1 1 1
93 CAST 0 0 1 0 0 -1 -1 1 0
82 OPPONENT_CAST 2 0 0 0 0 -1 -1 0 0
83 OPPONENT_CAST -1 1 0 0 0 -1 -1 1 0
84 OPPONENT_CAST 0 -1 1 0 0 -1 -1 1 0
85 OPPONENT_CAST 0 0 -1 1 0 -1 -1 1 0
87 OPPONENT_CAST 0 3 2 -2 0 -1 -1 0 1
89 OPPONENT_CAST 0 0 -3 3 0 -1 -1 0 1
91 OPPONENT_CAST -2 0 1 0 0 -1 -1 0 1
92 OPPONENT_CAST 2 1 -2 1 0 -1 -1 0 1
94 OPPONENT_CAST 3 -2 1 0 0 -1 -1 1 1
2 0 3 2 0
1 4 0 0 13

Nous souhaitons par exemple vérifier si une action BREW de la potion 0

    auto iss = fileToStringStream("resumeGameFiles/Compact/CompactActionBrew0");        MainHandler main;    main.parse(iss);        CompactState cs = CompactState::playerToCompactState(main.game.players[0]);        CompactState to = cs.doAction(main.game, main.game.players[0], CompactAction(Action::Type::BREW, 0));    uint64_t expected = CompactState::get(0b00001, 0b0  , 0b0        , 0b11110110, Inventory(0, 0, 0, 2));    //                                   (Brews  , Learn, CastLearned, spells    , Inventory           )        // Visual debug    cout << CompactState::getBitset(cs.getHashKey()) << endl;    cout << CompactState::getBitset(to.getHashKey()) << endl;    cout << CompactState::getBitset(expected) << endl;        EXPECT_EQ(            to.getHashKey(),            expected    );

À noter que le groupe de test Basic/False dans mon cas teste un simulateur de jeu (que je n'ai malencontreusement pas utilisé !)

Autant utiliser cg-brutaltester (que je n'ai pas testé non plus pour ce challenge !)

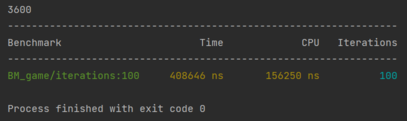
Benchmark

Benchmark

Le benchmark joue une centaine de fois la même partie d'une 50e de tours Couplé avec les tests, il est super facile de développer les optimisations

Bitwise opérations (section d'aide)

Voici les Shifts et Masks que j'utilise :

    static const int PLAYER_MAX_SPELL = 31;    static const uint64_t SHIFT_BREW = 0UL;    static const uint64_t MASK_BREW = 0b11111UL; // 5 bits mask    static const uint64_t SHIFT_LEARN = 5UL;    static const uint64_t MASK_LEARN = 0b111111UL; // 6 bits mask    static const uint64_t SHIFT_LEARNED = 11UL;    static const uint64_t MASK_LEARNED = 0b111111UL; // 6 bits mask    static const uint64_t SHIFT_SPELL = 17UL;    static const uint64_t MASK_SPELL = 0b1111111111111111111111111111111UL; // 31 bits mask    static const uint64_t SHIFT_INVENTORY = 48UL; // 64 bits - 16 for inventory    static const uint64_t MASK_INVENTORY_CASE = 0b1111UL; // 4 bits mask    static const uint64_t BIT_SIZE_INVENTORY_CASE = 4UL;

Réunification des éléments

Pour mes tests unitaires (cf TDD)

    static uint64_t get(uint64_t brews, uint64_t learns, uint64_t leanred, uint64_t spells, Inventory inventory) {        return brews               | (learns << SHIFT_LEARN)               | (leanred << SHIFT_LEARNED)               | (spells << SHIFT_SPELL)               | (inventory[0] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 0))               | (inventory[1] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1))               | (inventory[2] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 2))               | (inventory[3] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 3));    }

À chaque utilisation de l'opérateur left shift <<, on décale tous les bits vers la gauche d'un certain nombre de bits.

Lors du décalage, représenté par les x, chacun de ces bits vaudra 0

                                                                            0 0000
                                                                     000 000x xxxx ( l << SHIFT_LEARN ) // 5
                                                            0  0000 0xxx xxxx xxxx ( a << SHIFT_LEARNED ) // 11
                     0000 0000 0000 0000  0000 0001 0011 110x  xxxx xxxx xxxx xxxx ( s << SHIFT_SPELL ) // 17
               0000  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx ( i[0] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 0) // 48 + 4 * 0
          0100 xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx ( i[1] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1) // 48 + 4 * 1
     0000 xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx ( i[2] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 2) // 48 + 4 * 2
0010 xxxx xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx  xxxx xxxx xxxx xxxx ( i[3] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 3) // 48 + 4 * 3

Chacun de ces résultats peut donc être ajouté à l'autre grace à l'opérateur + ou même l'opérateur binaire |

0010 0000 0100 0000  0000 0000 0000 0000  0000 0001 0011 1100  0000 0000 0000 0000

Exemples d'opérations

Voici quelques exemples, si vous n'êtes pas trop à l'aise, je vous conseille très vivement de décomposer chaque opération.

Pour vérifier qu'un spell est castable (dans mon cas, s'il vaut 1), vous pouvez utiliser

  • Data désunifié (spells >> spellIndex) & 1
  • Data unifié (data >> (SHIFT_SPELL + spellIndex)) & 1

Si mon action me demande de caster mon 2eme spell, c'est-à-dire mettre son bit à 0

  • Data désunifié spells &= ~(1UL << spellIndex) // spellIndex == 2
  • Data unifié spells &= ~(1UL << (SHIFT_SPELL + spellIndex)) // spellIndex == 2

Si mon action me demande de brew la 2eme potion, c'est-à-dire mettre son bit à 1

  • Data désunifié brews |= (1L << spellIndex) // spellIndex == 2
  • Data unifié data |= (1L << (SHIFT_BREW + spellIndex)) // spellIndex == 2

Pour modifier mon inventaire, je peux faire ainsi

  • Data désunifié inventory[1] += recipe[1]
  • Data unifié data = (data & ~(MASK_INVENTORY_CASE << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1))) | (inventory[1] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1)

L'exemple sur la data unifié est un petit peu complexe, alors je vais la décomposer.

uint64_t data = 0b0010000001000000000000000000000000000001001111000000000000000000;
// 0010 0000 0100 0000  0000 0000 0000 0000  0000 0001 0011 1100  0000 0000 0000 0000

uint64_t mask = MASK_INVENTORY_CASE << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1);
// 0000 0000 1111 0000  0000 0000 0000 0000  0000 0000 0000 0000  0000 0000 0000 0000
mask ~= mask;
// 1111 1111 0000 1111  1111 1111 1111 1111  1111 1111 1111 1111  1111 1111 1111 1111

data &= mask;
// 0010 0000 0000 0000  0000 0000 0000 0000  0000 0001 0011 1100  0000 0000 0000 0000


uint64_t toReplace = (inventory[1] << (SHIFT_INVENTORY + BIT_SIZE_INVENTORY_CASE * 1); // inventory[1] == 5
// 0000 0000 0101 0000  0000 0000 0000 0000  0000 0000 0000 0000  0000 0000 0000 0000

data |= toReplace 
// 0010 0000 0101 0000  0000 0000 0000 0000  0000 0001 0011 1100  0000 0000 0000 0000
>